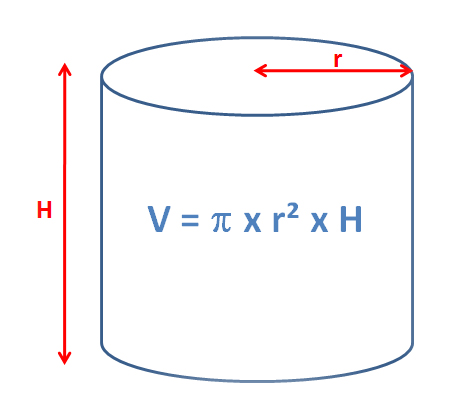
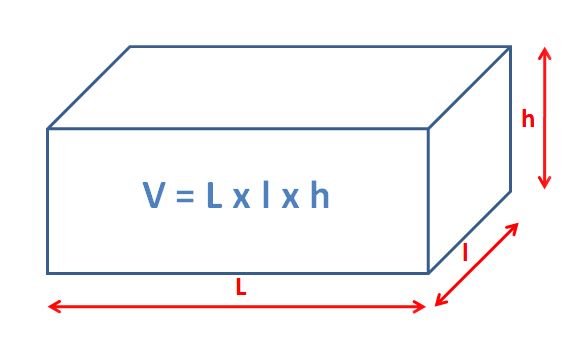
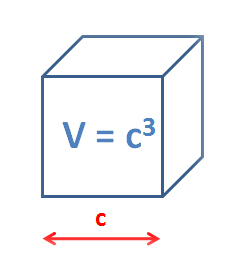
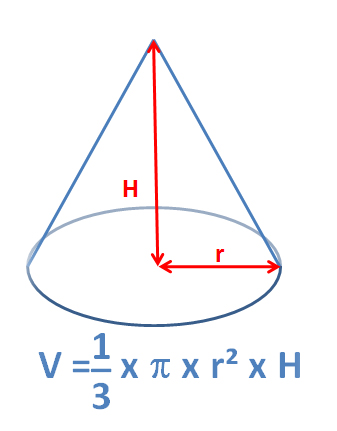
Pour les volumes qui ressemblent à un cône ou à une pyramide, on calcule la base qu’on divise par 3 puis on multiplie par la hauteur. V = 1/3 x B x H avec B l’aire de la base et H la hauteur.
Ainsi, pour une pyramide avec une base carrée, le volume vaut V = 1/3 x c² x H.
Une pyramide dont la base serait rectangulaire, le volume serait alors V = 1/3 x L x l x H.
etc…
Pour calculer le volume du cylindre, on commence par calculer l’aire du disque qui forme la base puis on la multiplie par la hauteur.
Le volume du parallélépipède est égal au produit de la longueur par la largeur et par la hauteur. Pour beaucoup de volume, il suffit de calculer l’aire de la base et de la multiplier par la hauteur.
Si L est la longueur, si l est la largeur et si h est la hauteur, alors le volume V = L x l x h
Pour calculer le volume d’un cube, il suffit de connaître son côté et de l’élever au… cube !
Si c est la mesure du côté, alors le volume V = c x c x c = c 3
En électricité, le courant est créé par le déplacement des électrons d’un bout à l’autre d’un conducteur. On dit que ce courant est alternatif (en anglais, alternating current ou AC qu’on retrouve sur certains appareils) si les électrons se déplacent alternativement dans un sens puis dans un autre.
Un courant alternatif est sinusoïdal si son intensité est une fonction sinus du temps : i(t)=I.sin(ωt+φ)
ω est appelée la pulsation (rad/s)
φ représente la phase du courant sinusoïdal
On obtient la fréquence en Hertz du courant ainsi : f=2π/ω et la période :T=1/f=ω/2π
Le périmètre du triangle ABC se calcule selon la formule : P=AB+BC+AC
Si on note H la hauteur issue de A, l’aire du triangle ABC s’écrit alors : Aire=AH.BC
Le périmètre du parallélogramme ABCD se calcule selon la formule : P=2.(AB+BC)
Si on note H la hauteur issue de A, l’aire du parallélogramme ABCD s’écrit : Aire=AB.AH
Le périmètre du rectangle ABCD se calcule selon la formule : P=2.(AB+BC)
L’aire du rectangle ABCD s’écrit : Aire=AB.BC
Le périmètre du carré ABCD se calcule selon la formule : P=4.AB
L’aire du carré ABCD s’écrit : Aire=AB²
Soit un triangle quelconque ABC et (DE) une droite parallèle à (BC) tel que D se trouve sur (AB) et E sur (AC) :
Le théorème de Thalès affirme que dans cette configuration, on a les égalités suivantes :
Le théorème fonctionne également si la construction se présente ainsi :
Réciproque du théorème de Thalès :
Soit ABC un triangle, D un point de la droite (AB) et E un point de la droite (AC), si on a les égalités :
alors les droites (BC) et (DE) sont parallèles.
